RSALearner - An interactive visualization for learning the RSA Algorithm
The RSALearner app is an interactive visualization of the RSA algorithm and cryptosystem using Python, Jupyter Notebook and Widgets. This tutorial explains the usage and step-by-step implementation of the app. The emphasis is on key generation and encryption / decryption, the mathematically correct generation of the prime numbers p, q, the RSA module n, Eulers function phi, public key e, private key d and applying the required steps and formulas for encryption and decryption of alphanumerical messages.
Motivation
Asymmetric cryptosystems use different keys for encoding and decoding, more precisely: each key is a key pair consisting of a Public Key PU and a Private Key PR. The public key PU of the receiver is used by the sender for encoding a message, and the private key PR of the receiver is used by its owner to decode the message. When learning RSA, beginners are often confused about the order of steps involved in key generation, if the generated keys are really correct, who owns which key and uses it for what.
Jupyter Notebook visualizations are useful because they can be easily shared with students and combine documentation and code blocks in a natural way. With Jupyter Widgets you can add interactions and create a GUI in which the key generation, encryption and decryption can be explored step-by-step.
Overview
The user interface is shown in an output cell at the end of the Jupyter Notebook. In order to run it in Google Colab, save a copy of the existing Notebook RSALearner.ipynb in your own Google Colab and run it there.
1 RSALearner Usage
| Top |
The RSALearner app has two tabs: Tab 1 "Key generation" is the user interface for creating the receiver's key pair, Tab 2 "Encryption" is the user interface for encrypting and decrypting a message using the previosly created key pair.
Tab 1: Key Generation
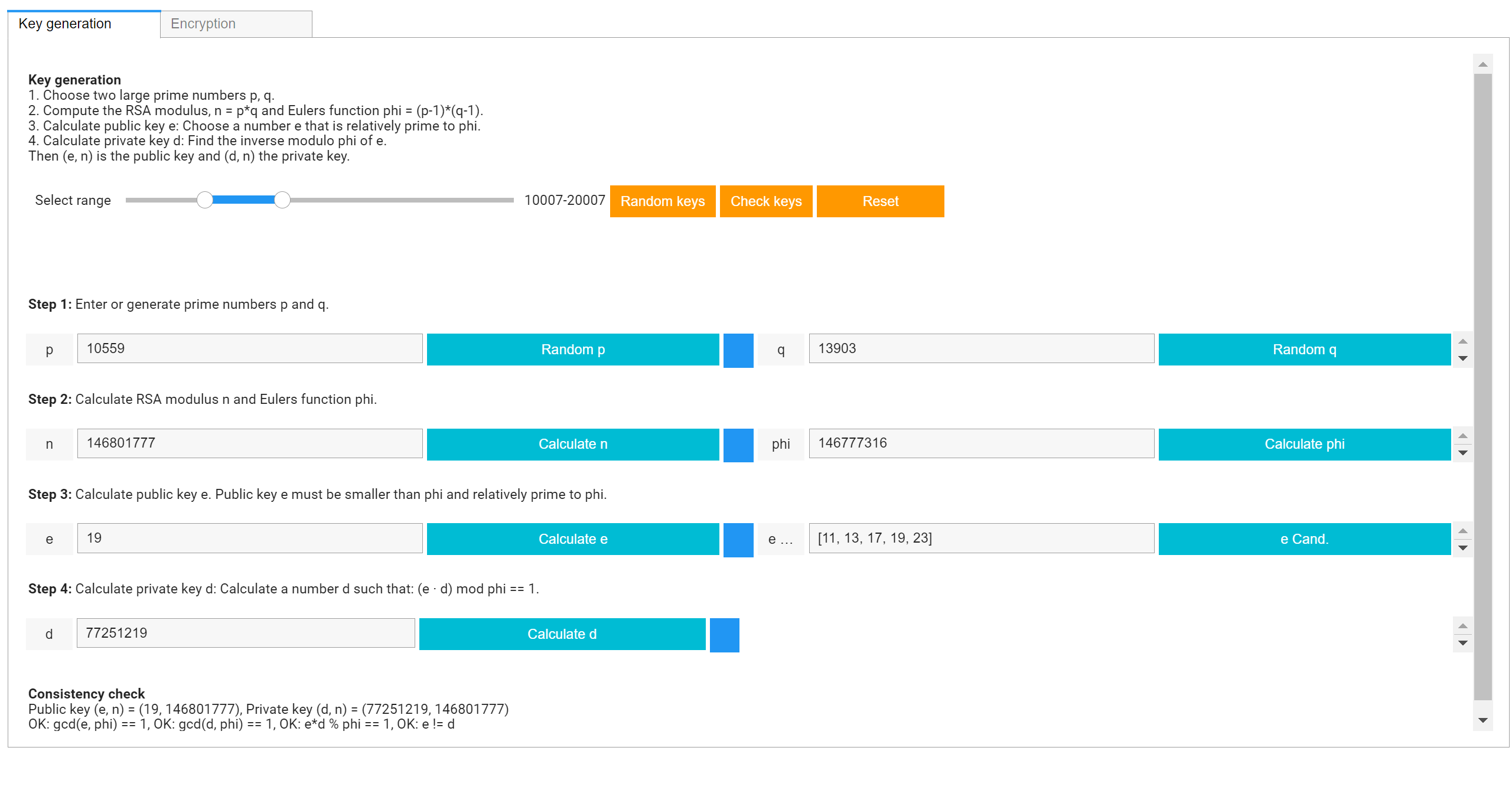
Tab 2: Encryption
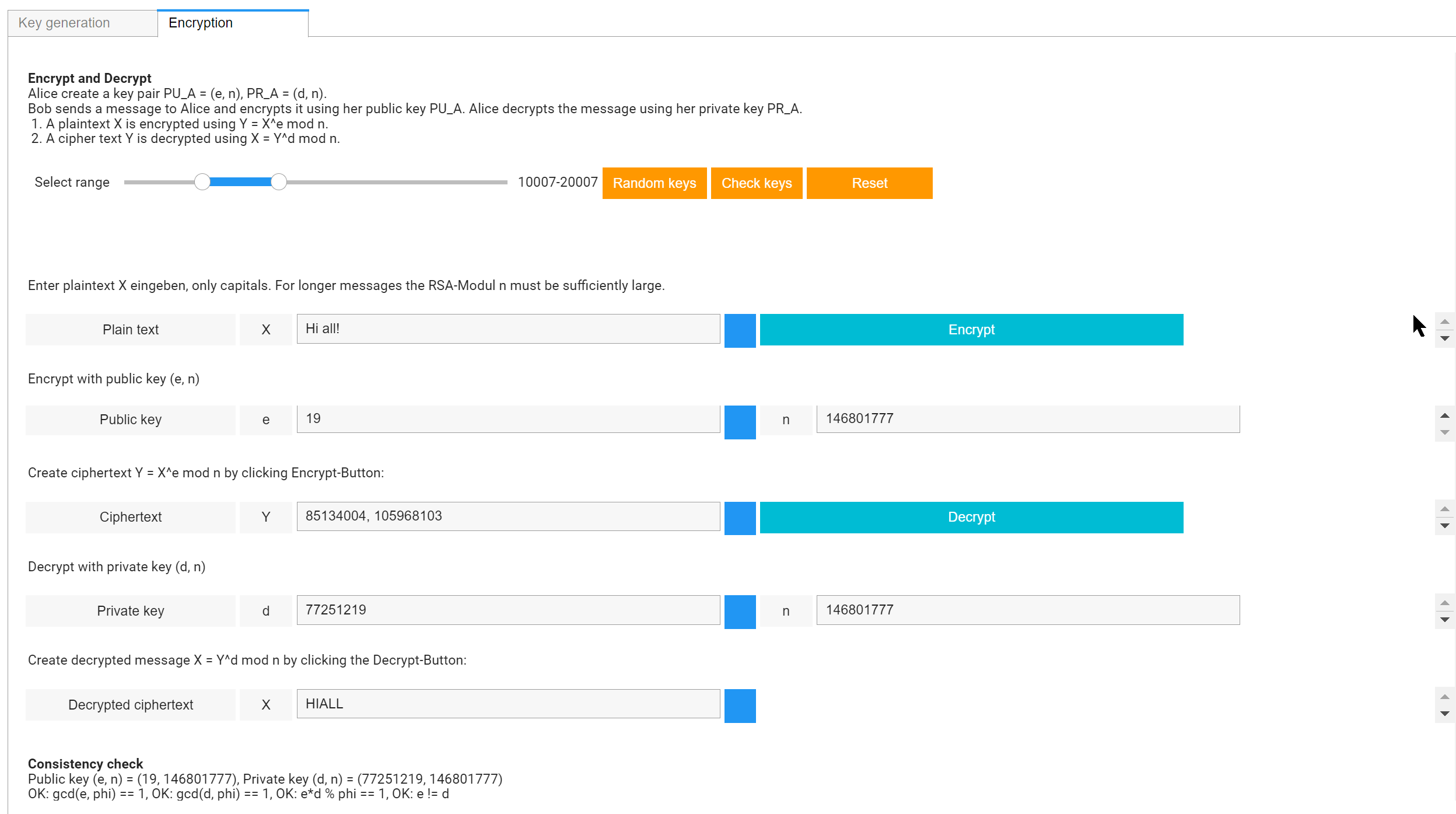
1-1 Key Generation
Tab 1 "Key generation" leads through the steps for generating a valid key pair. Start by entering your own prime numbers p, q or by generating random numbers p, q within a given range that is chosen via a RangeSlider.
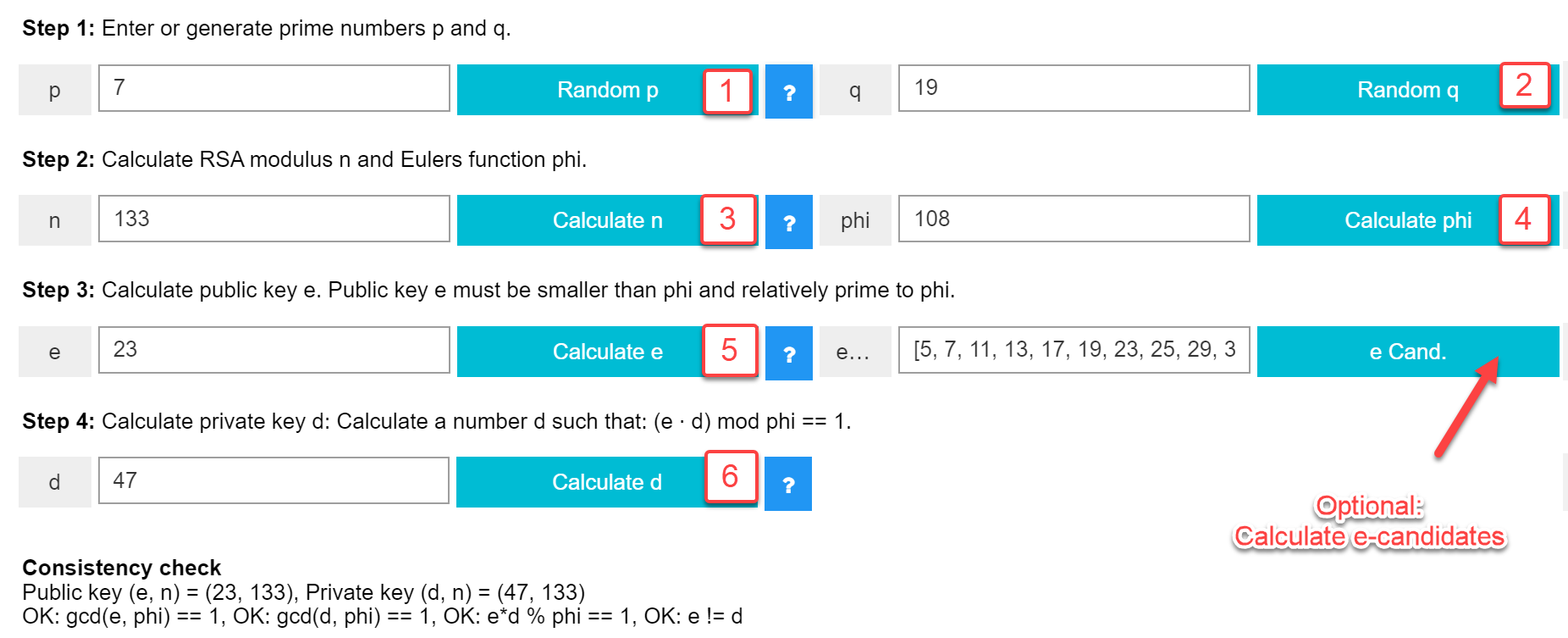
Step 1. Choose two prime numbers p, q. Random numbers p and q can be entered manually or generated by using the buttons
"Random p", "Random q", then they will be in the selected range.
Step 2. Compute the RSA modulus, n = p*q and Eulers function phi = (p-1)*(q-1) by using the respective buttons.
Step 3. Calculate public key e: Choose a number e that is relatively prime to phi.
In this step, the public key is chosen randomly from a list of candidates for e.
Step 4. Calculate private key d: Determine the inverse modulo phi of e, that is a number d, such that d*e mod phi == 1.
The inverse modulo phi of e is found using the extended euclidian algorithm.
Then (e, n) is the public key and (d, n) the private key.
For a quick start, you can generate a key pair automatically by clicking the button "Random keys".
1-2 Encryption and Decryption
As alphabet for plaintext messages we use ABCDEFGHIJKLMNOPQRSTUVWXYZ. Plaintext messages should contain only alphanumeric characters. We actually remove all other characters from the plaintext message.
Encryption
For encryption, enter a plaintext message containing only alphanumeric characters,
for example "Hello World" or "Have a nice day", then click the Encrypt-button.
The encrypted message will appear as a list of numbers in the Ciphertext field.
Encryption is done like this: first, the plaintext message is converted into a numerical plaintext using ASCII coding.
Then, this large number is chopped into blocks of length 8.
Each of these blocks X is encrypted using the formula X^e mod n, resulting in the list of numbers
displayed next to Y.
Decryption
For decryption of the previously encrypted ciphertext Y press the "Decrypt" button.
Each block Y_i of the cipher list Y is decrypted using the formula Y_i^d mod n and the
resulting numbers are converted back to alphanumeric characters.
2 RSALearner Implementation
| Top |
This Python implementation of the RSA cryptosystem uses a set of helper functions that are explained below. The implementation makes some didactically motivated simplifications. A real-life working implementation of RSA encryption will consider further modifications such as padding. Before starting, you need to have working Jupyter Notebook installation on your computer, that can be obtained via an Anaconda installation. Or, you can skip the local installation and simply run the Google Colab script as described above.
2-1 Required packages
For creating an interactive GUI in Jupyter Notebook we need the classes and methods of the ipywidgets-package. Also, we need some functions from the math, numpy, random, re and sympy packages so that we don't have to write our own utility functions. The packages can be installed as usually using pip or conda commands, for example pip install re or conda install re.
- random - a Python library for creating random numbers.
- sympy - a Python library for symbolic mathematics.
- re - a Python library regular expressions. We use this for filtering the plaintext for characters that are not in our alphabet.
import numpy as npimport math #import random # Random number creationimport re # Regular expressionsfrom sympy import * # isprimefrom ipywidgets import Layout, Label, Text, HTMLfrom ipywidgets import Button, SelectionRangeSliderfrom ipywidgets import HBox, VBox, GridspecLayout, Tab
2-2 RSA Helper Functions
| Top |
In order to implement the four steps of key generation we need some helper functions: get_primes(), get_e(), extended_euclid() and modular_inverse(). In a first step, we show their usage with a predefined set of values, for which we know the expected output: p = 7, q = 19, n = 133, phi = 108, e = 23, d = 47.
- Function get_primes(min=7, max=100):
Calculate all prime numbers in the given range. This function is used in Step 1. - Function get_e(phi):
Calculate candidates for the public key e. This function is used in Step 3. For very large phi this may take some time, so we restrict the calculation to max. 100 candidates. - Functions extended_euclid(phi, e) and modular_inverse(e, phi):
Carry out the extended euclidian algorithm and calculate the modular inverse of e modulo phi.
The well known Euclidian algorithm calculates the greatest common divisor of two natural numbers. In addition to the greatest common divisor gcd(a, b) of two integer numbers a and b, the Extended Euclidean algorithm also calculates two integers s and t that satisfy the equation gcd(a, b) = s * a + t * b .
In RSA key generation, the Extended Euclidean algorithm is used to calculate the private key d as the modular inverse of d modulo phi. That is, for given phi and e, one has to find two numbers d and k such that d * e + k * phi = gcd(phi, e) = 1.
getprimes()
def get_primes(min=7, max=100):'''Calculate all prime numbers in the given range '''primes = []for i in range(min, max):if isprime(i):primes.append(i)return primes
Test function get_primes()
The parameters min, max will be chosen using a SelectionRangeSlider
primes = get_primes(min = 5000, max = 10000) print(primes)
Function get_e()
We restrict the calculation of e candidates to max. 100 numbers.
def get_e(phi):'''Calculate candidates for the public key e '''e_candidates = []for i in range(7, phi-1):if math.gcd(i, phi) == 1:e_candidates.append(i)if len(e_candidates) == 100:breakreturn e_candidates
Test function get_e()
In this example, we calculate and print the e candidates for phi = 108.
e_candidates = get_e(phi = 108)print(e_candidates)# Output:# [5, 7, 11, 13, 17, 19, 23, 25, 29,# 31, 35, 37, 41, 43, 47, 49, 53, 55,# 59, 61, 65, 67, 71, 73, 77, 79, 83,# 85, 89, 91, 95, 97, 101, 103]
Function modular_inverse()
def extended_euclid(phi, e):''' Carry out the extended euclidian algorithm'''if e == 0:return (1, 0, phi)else :k, d, gcd = extended_euclid(e, phi % e)return d, k - d * (phi // e), gcddef modular_inverse(e, phi):''' Calculate the modular inverse of e modulo phi '''k, d, gcd = extended_euclid(phi, e)if gcd == 1 :return d % phielse:return None
Test function modular_inverse()
phi = 108e = 23k, d, gcd = extended_euclid(phi, e)d = modular_inverse(e, phi)print("k, d, gcd = ", k, d, gcd )print("d = " , d)## Output:# k, d, gcd = -10 47 1# d = 47
In order to implement the steps of encryption / decryption we use the helper functions get_ascii(), to_ascii(), to_block(), to_letters() and encrypt(). Before using them in the widgets, we test them separately.
- Functions for ASCII encoding
get_ascii() returns a dictionary for ASCII coding our alphabet. to_ascii() converts a text to ascii coding. - Functions for splitting and joining
- Functions for encryption / decryption
Functions for ASCII encoding
get_ascii(), to_ascii()
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"def get_ascii():'''Return a dict. for ASCII {A = 65, B = 66, ...}'''ascii = dict()offset = 65for l in alphabet:ascii[l] = offsetoffset += 1return asciidef to_ascii(text):ascii = get_ascii()s = "".join([str(ascii[l]) for l in text.upper()])return s
Test functions for ASCII encoding
get_ascii(), to_ascii()
ascii = get_ascii()print('ASCII-Dict\n', ascii)plaintext = 'HelloWorld'ascii_encoded = to_ascii(plaintext)print('ASCII-encoded text\n', ascii_encoded)## Output:#ASCII-Dict# {'A': 65, 'B': 66, 'C': 67, 'D': 68, 'E': 69,# 'F': 70, 'G': 71, 'H': 72, 'I': 73, 'J': 74,# 'K': 75, 'L': 76, 'M': 77, 'N': 78, 'O': 79,# 'P': 80, 'Q': 81, 'R': 82, 'S': 83, 'T': 84,#'U': 85, 'V': 86, 'W': 87, 'X': 88, 'Y': 89, 'Z': 90}#ASCII-encoded text#72697676798779827668
Functions for splitting and joining
to_block(), to_letters()
def to_block(text_num):''' Split a numerical string into chunks of 8 '''cp = str(text_num)blocklist = []while len(cp) > 7:blocklist.append(cp[:8])cp = cp[8:]if cp:blocklist.append(cp)return blocklistdef to_letters(lst):''' Transform numerical message back to alphabet'''s = "".join([str(block) for block in lst])plaintext = ""while s:plaintext += alphabet[int(s[:2])-65].upper()s = s[2:]return plaintext
Test functions for splitting and joining
to_block(), to_letters()
Output of the testtext = 'HelloWorld'print('Text: ', text)text_num = to_ascii(text)print('Text, ASCII-Encoded: ',text_num)# Test to_block: text_num -> list_numlist_num = to_block(text_num)print('Text, Blocks of 8: ', list_num)# Test block_to_lettersplaintext = to_letters(list_num)print('Text, Back to letters:', plaintext)

Functions for encryption /decryption
encrypt()
The same function encrypt is used for encryption and decryption.
Each of the blocks X from plaintext_list is encoded using X ^ e mod n. Each of the blocks Y from cipher_list is encoded using Y ^ d mod n.
def encrypt(lst, key, n):''' Encrypt / decrypt a list of blocks '''retlist = []for block in lst:retlist.append(pow(int(block), key, n))return retlist
Test functions for encryption / decryption
encrypt()
Output of the testd = 109045109 # public keye = 29 # private keyn = 158141033 # RSA modulusplaintext = 'HelloWorld'print('Text: ', text)plaintext_num = to_ascii(text)print('Text, ASCII-Encoded: ', plaintext_num)# Chop the number message into 8-digit blocksplaintext_list = to_block(plaintext_num)# ENCRYPTION with encryptcipher_list = encrypt(plaintext_list, e, n)print('Cipher List', cipher_list)# DECRYPTION, also with encryptplaintext_list2 = encrypt(cipher_list, d, n)plaintext2 = to_letters(plaintext_list2)print('Decrypted message: ', plaintext2)

3 Interactive GUI with Jupyter Widgets
| Top |
The graphical user interface uses container widgets HBox, VBox, GridspecLayout, Tab, string widgets Label, Text, HTML and buttons. We introduced some helper functions with the intention to simplify the creation of GUI elements with standardized styles. For example, the function create_button_def creates the default buttons that have width 25% of their container and all have the same color (Bootstrap-style 'info').
Functions for creating button and text widgets
create_button(), create_text()
def create_button(description, button_style='', width='auto', height='30px', icon=''):btn_layout = Layout(width=width, height=height)btn = Button(description=description, button_style=button_style,layout=btn_layout, icon = icon)def create_button_def(description):return create_button(description, button_style='info', width='25%')return btndef create_label(text, width='7%'):label_layout = Layout(width=width)return Label(value=text, layout=label_layout)def create_text(text='', placeholder='', width='30%'):text_layout = Layout(width=width)return Text(value=text, placeholder=placeholder, layout=text_layout)def create_html(text, width='auto', height='auto'):html_layout = Layout(width=width, height = height)return HTML(value=text, layout=html_layout)
Test functions for creating button and text widgets
create_button(), create_text()
Outputlabel_p = create_button('p', '', width='50px')text_p = create_text(placeholder='Enter p')btn_p = create_button_def('Random p ')btn_p.tooltip = 'Generate random prime p.'display(HBox([label_p, text_p, btn_p]))

Tools & References
| Top |
- [1] RSA-Overview on Wikipedia.
- [2] Extended Euclidian Algorithm on Wikipedia.
- [3] Python Cheatsheet.
- [4] Jupyter Notebook Widgets.
- [5] Jupyter Notebooks verwenden (in German).
- [6] Jupyter Notebook Widgets verwenden (in German).